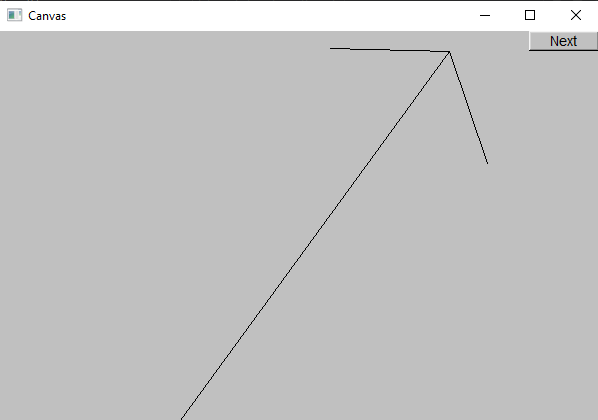
Aim - Create a C++ program to draw an arrow:

• between 2 given coordinates
• arms of length as a given ratio to its body length
• arms at specified incline to the body

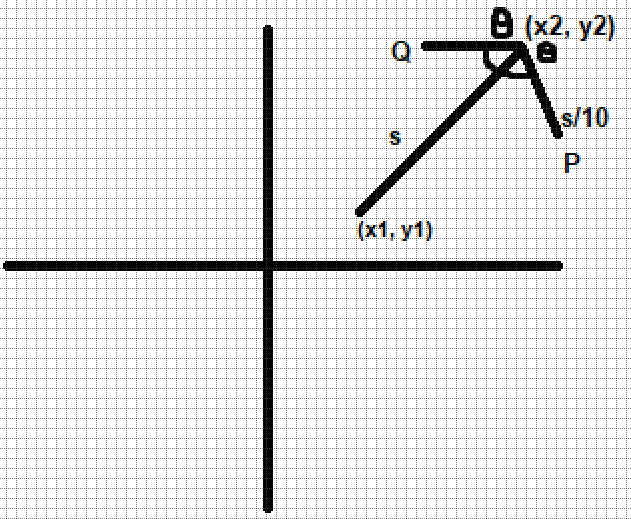
Given:

• Start point of arrow as (x1, y1) and end point (x2, y2). Eg: (2, 3) and (10, 100)
• Ratio provided = x : y. Eg 1:10
• Incline of arrow arms (in degrees) = θ. Eg: θ=67

Attempt 1

Attempt 1 relies on individually calculating the slope of all 3 lines and finding points of the arrow by combining equations of distance formula, tangent slope formula and solving based on cases.

It is pretty evident that the approach is innefficient and also needlessly complicated. At this point I can't even understand what I was even trying to do :/

Arrow.cpp

void Arrow::draw_lines() const {
    Line::draw_lines();
    const Point top = (dir == 's') ? start : end;
    const double distance = sqrt(pow((start.x - end.x), 2) + pow((start.y - end.y), 2));    
    const double arrow_len = distance / 10;
    const double radians = (angle)*(PI/180);
    
    const double stick_slope = (end.y - start.y) / float(end.x - start.x);

    const double p_slope = ((-stick_slope) - tan(radians)) / ((tan(radians)*stick_slope) - 1);

    const double p_a = 1 + pow(p_slope, 2);
    const double p_b = (-2*top.x) - (2 * (top.x) * pow(p_slope, 2));
    const double p_c = -pow(arrow_len, 2) + pow(top.x, 2) + pow(top.x, 2)*pow(p_slope, 2);
    const double p_disc = sqrt(pow(p_b, 2) - 4*p_a* p_c);
    const double p_x_1 = (-p_b + p_disc) / (2 * p_a);
    const double p_x_2 = (-p_b - p_disc) / (2 * p_a);

    const double p_y_1 = p_slope * p_x_1 - p_slope * top.x + top.y;
    const double p_y_2 = p_slope * p_x_2 - p_slope * top.x + top.y;

    double p_x;
    double p_y;

    if (abs(p_y_1) > abs(top.y)) {
        p_x = p_x_2;
        p_y = p_slope * p_x - p_slope * top.x + top.y;
    }
    else {
        p_x = p_x_1;
        p_y = p_slope * p_x - p_slope * top.x + top.y;
    }

    std::cout << "(" << p_x << ", " << p_y  << ")\n";

    const double q_slope = (stick_slope - tan(radians)) / (stick_slope + 1);

    const double q_a = 1 + pow(q_slope, 2);
    const double q_b = (-2 * top.x) - (2 * (top.x) * pow(q_slope, 2));
    const double q_c = -pow(arrow_len, 2) + pow(top.x, 2) + pow(top.x, 2) * pow(q_slope, 2);
    const double q_disc = sqrt(pow(q_b, 2) - 4 * q_a * q_c);
    const double q_x_1 = (-q_b + q_disc) / (2 * q_a);
    const double q_x_2 = (-q_b - q_disc) / (2 * q_a);


    const double q_y_1 = q_slope * q_x_1 - q_slope * top.x + top.y;
    const double q_y_2 = q_slope * q_x_2 - q_slope * top.x + top.y;


    double q_x;
    double q_y;


    if (abs(q_y_1) > abs(top.y)) {
        q_x = q_x_2;
        q_y = q_slope * q_x - q_slope * top.x + top.y;
    }
    else {
        q_x = q_x_1;
        q_y = q_slope * q_x - q_slope * top.x + top.y;
    }

    std::cout << "(" << q_x << ", " << q_y << ")\n";
    std::cout << "(" << start.x << ", " << start.y << ")\n";
    std::cout << "(" << end.x << ", " << end.y << ")\n";

    fl_line(top.x, top.y, p_x, p_y);
    fl_line(top.x, top.y, q_x, q_y);
}

A Better Approach

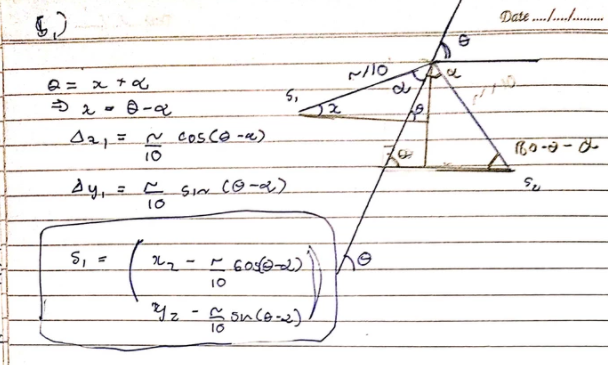
An easier method to draw the arrow would be to:

1. Calculate the distance between the 2 points
2. Calculate the slope of the line. Note: use atan2 for getting the angle correctly for all quadrants
3. Calculate the x and y coordinates of the arrow arm tips as such

/**
 * x-coordinate of tip on the left of the arrow
 * Horizontal Distance between join of arms at the top of the arrow 
   and tip of the left arm is ``r/10*cos(theta-alpha)``
 */

const double s1_x = end.x - (distance / fraction) * cos(slope_angle - incline); 

/**
 * y-coordinate of tip on the left of the arrow
 * Vertical Distance between join of arms at the top of the arrow 
   and tip of the left arm is ``r/10*sin(theta-alpha)``
 */

const double s1_y = end.y - (distance / fraction) * sin(slope_angle - incline);

// For the right arm the distance from the joins is added horizontally and subtracted vertically

Final Code

namespace Graph_lib {
    Arrow::Arrow(Point start, Point end, double angle) : start{ start }, end{ end }, 
    Line(start, end), angle{ angle } {
        if (angle >= 90 || angle <= 0) throw std::runtime_error("Invalid Angle");
    }


    void Arrow::draw_lines() const {
        Line::draw_lines();
        const double distance = sqrt(pow(start.x - end.x, 2) + pow(start.y - end.y, 2));
        const double slope_angle = atan2((end.y - start.y) , (end.x - start.x));
        const double incline = deg_to_rad(angle);


        const double s1_x = end.x - (distance / fraction) * cos(slope_angle - incline);
        const double s1_y = end.y - (distance / fraction) * sin(slope_angle - incline);
        
        const double s2_x = end.x + (distance / fraction) * cos(PI - slope_angle - incline);
        const double s2_y = end.y - (distance / fraction) * sin(PI - slope_angle - incline);


        std::cout << s1_x << " " << s1_y << "\n";
        std::cout << s2_x << " " << s2_y << "\n";


        fl_line(end.x, end.y, s1_x, s1_y);
        fl_line(end.x, end.y, s2_x, s2_y);
    }
};

Result

The arrow plots for any arbitrary set of points and angle after running the code

Eg: Arrow arrow{ Point{300, 375}, {107, 201}, 68 };